Existence of Time-Scale Class of Three Dimensional Fractional Differential Equations

Article Sidebar

PDF
Cite as:
Rabha W. Ibrahim, Maslina Darus, Existence of Time-Scale Class of Three Dimensional Fractional Differential Equations, Int. J. Anal. Appl., 17 (3) (2019), 396-405.

Main Article Content

Rabha W. Ibrahim, Maslina Darus

Abstract

The holomorphic results for fractional differential operator formals have been established. The analytic continuation of these outcomes has been studied for the fractional differential formal

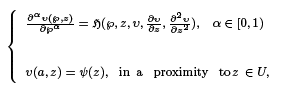
where U is the open unit disk. The benefit of such a problem is that a generalization of two significant problems: the Cauchy problem and the diffusion problem. Moreover, the analytic solution is given inside the open unit disk, this leads to discuss the solution geometrically. The upper bound of outcomes is determined by suggesting a majorant analytic function in U (for two functions characterized by a power series, a majorant is the summation of a power series with positive coefficients which are not less than the absolute values of the conforming coefficients of the assumed series). This technique is very useful in approximation theory.

Article Details

References

  1. M. Bohner, A. Peterson, Dynamic equations on times scale, Birkhauser Boston, Boston, MA, 2001.
  2. A. A. Kilbas, H. M. Srivastava and J.J. Trujillo, Theory and applications of fractional differential equations. North-Holland, Mathematics Studies, Elsevier 2006.
  3. J. Sabatier, O. P. Agrawal, J. A. Tenreiro Machado, Advance in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering, Springer, 2007.
  4. D. Baleanu, B. Guvenc Ziya, J. A. Tenreiro, New Trends in Nanotechnology and Fractional Calculus Applications, Springer, 2009.
  5. R. W. Ibrahim, Existence and uniqueness of holomorphic solutions for fractional Cauchy problem, J. Math. Anal. Appl. 380 (2011), 232-240.
  6. R. W. Ibrahim, On holomorphic solutions for nonlinear singular fractional differential equations, Comput. Math. Appl. 62 (3) (2011), 1084-1090.
  7. R. W. Ibrahim, Generalized Ulam-Hyers stability for fractional differential equations, Int. J. Math. 23 (5) (2012), Art. ID 1250056.
  8. R. W. Ibrahim, The fractional differential polynomial neural network for approximation of functions, Entropy 15 (10) (2013), 4188-4198.
  9. R. W. Ibrahim, et al., Fractional differential texture descriptors based on the Machado entropy for image splicing detection. Entropy 17 (7) (2015), 4775-4785.
  10. R. W. Ibrahim and M. Darus, Analytic Study of Complex Fractional Tsallis Entropy with Applications in CNNs, Entropy 20 (10) (2018), Art. ID 722.