Instabilities and Stabilities of Additive Functional Equation in Paranormed Spaces

Article Sidebar

PDF
DOI: https://doi.org/10.28924/2291-8639-22-2024-3
Published: Jan 3, 2024
Cite as:
S. Karthikeyan, J. Venkatesan, N. Vijaya, G. Chitra, G. Ganapathy, Instabilities and Stabilities of Additive Functional Equation in Paranormed Spaces, Int. J. Anal. Appl., 22 (2024), 3.

Main Article Content

S. Karthikeyan, J. Venkatesan, N. Vijaya, G. Chitra, G. Ganapathy

Abstract

In this paper, we solve the general solution in vector space and prove the Hyers-Ulam stability of the following additive functional equation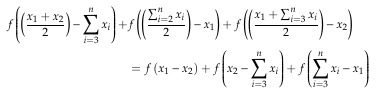

in paranormed spaces by using the direct and fixed point methods. Also we present its pertinent counter examples for instabilities.

Article Details

References

  1. M. Adam, Alienation of the Quadratic and Additive Functional Equations, Anal. Math. 45 (2019), 449–460. https://doi.org/10.1007/s10476-019-0869-1.
  2. T. Aoki, On the Stability of the Linear Transformation in Banach Spaces, J. Math. Soc. Japan. 2 (1950), 64–66. https://doi.org/10.2969/jmsj/00210064.
  3. M. Arunkumar, S. Karthikeyan, Solution and Stability of n-Dimensional Additive Functional Equation, Int. J. Appl. Math. 25 (2012), 163–174.
  4. G. Asgari, Y. Cho, Y. Lee, M.E. Gordji, Fixed Points and Stability of Functional Equations in Fuzzy Ternary Banach Algebras, J. Inequal Appl. 2013 (2013), 166. https://doi.org/10.1186/1029-242x-2013-166.
  5. L. Cadariu, V. Radu, Fixed Points in Generalized Metric Space and the Stability of a Quartic Functional Equation, Bul. Stiint. Univ. Politeh. Timis. Ser. Mat. Fiz. 50 (2005), 25–34.
  6. M.E. Gordji, H. Khodaei, M. Kamyar, Stability of Cauchy-Jensen Type Functional Equation in Generalized Fuzzy Normed Spaces, Comput. Math. Appl. 62 (2011), 2950–2960. https://doi.org/10.1016/j.camwa.2011.07.072.
  7. M.E. Gordji, H. Khodaei, Th.M. Rassias, Fixed Points and Generalized Stability for Quadratic and Quartic Mappings in C ∗ -Algebras, J. Fixed Point Theory Appl. 17 (2015), 703–715. https://doi.org/10.1007/s11784-015-0251-2.
  8. H. Fast, Sur la Convergence Statistique, Colloq. Math. 2 (1951), 241–244. http://eudml.org/doc/209960.
  9. J.A. Fridy, On Statistical Convergence, Analysis, 5 (1985), 301–313.
  10. Z. Gajda, On Stability of Additive Mappings, Int. J. Math. Math. Sci. 14 (1991), 431–434.
  11. P. Gavruta, A Generalization of the Hyers-Ulam-Rassias Stability of Approximately Additive Mappings, J. Math. Anal. Appl. 184 (1994), 431–436. https://doi.org/10.1006/jmaa.1994.1211.
  12. D.H. Hyers, On the Stability of the Linear Functional Equation, Proc. Natl. Acad. Sci. U.S.A. 27 (1941), 222–224. https://doi.org/10.1073/pnas.27.4.222.
  13. S. Jung, Local Stability of the Additive Functional Equation, Glasnik Mat. 38 (2003), 45–55.
  14. S. Karakus, Statistical convergence on probalistic normed spaces, Math. Commun. 12 (2007), 11–23.
  15. K. Subramani, C. Park, J. Rassias, Stability of quartic functional equation in paranormed spaces, Math. Anal. Contemp. Appl. 3 (2021), 48–58. https://doi.org/10.30495/maca.2021.1924046.1001.
  16. S. Karthikeyan, C. Park, P. Palani, T.R.K. Kumar, Stability of an Additive-Quartic Functional Equation in Modular Spaces, J. Math. Comput. Sci. 26 (2021), 22–40. https://doi.org/10.22436/jmcs.026.01.04.
  17. M. Khanehgir, Stability of the Jensen’s Functional Equation in Multi-Fuzzy Normed Spaces, Iran. J. Fuzzy Syst. 14 (2017), 105–119. https://doi.org/10.22111/ijfs.2017.3258.
  18. E. Kolk, The Statistical Convergence in Banach Spaces, Tartu Ul Toime. 928 (1991), 41–52.
  19. Y.H. Lee, G. Kim, Generalized Hyers–Ulam Stability of the Additive Functional Equation, Axioms. 8 (2019), 76. https://doi.org/10.3390/axioms8020076.
  20. B. Margolis, J. B. Diaz, A Fixed Point Theorem of the Alternative for Contractions on a Generalized Complete Metric Space, Bull. Amer. Math. Soc. 74 (1968), 305–309.
  21. M. Mursaleen, λ-Statistical Convergence, Math. Slovaca. 50 (2000), 111–115. http://dml.cz/dmlcz/136769.
  22. M. Mursaleen, S.A. Mohiuddine, On Lacunary Statistical Convergence With Respect to the Intuitionistic Fuzzy Normed Space, J. Comput. Appl. Math. 233 (2009), 142–149. https://doi.org/10.1016/j.cam.2009.07.005.
  23. A. Niazi Motlagh, The Generalized Hyers–ulam Stability of Derivations in Non-Archimedean Banach Algebras, Math. Anal. Cont. Appl. 2 (2020), 17–22. https://doi.org/10.30495/maca.2020.679852.
  24. C. Park, J.M. Rassias, A. Bodaghi, S.O. Kim, Approximate Homomorphisms From Ternary Semigroups to Modular Spaces, Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat., RACSAM. 113 (2018), 2175–2188. https://doi.org/10.1007/s13398-018-0608-7.
  25. C. Park, M.Th. Rassias, Additive functional equations and partial multipliers in C ∗ -algebras, Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat., RACSAM. 113 (2018), 2261–2275. https://doi.org/10.1007/s13398-018-0612-y.
  26. V. Radu, The Fixed Point Alternative and the Stability of Functional Equations, Fixed Point Theory. 4 (2003), 91–96.
  27. M. Ramdoss, D. Pachaiyappan, H. Dutta, Functional Equation and Its Modular Stability With and Without ∆p Condition, Filomat. 34 (2020), 919–930. https://doi.org/10.2298/fil2003919r.
  28. J. M. Rassias, On approximately of approximately linear mappings by linear mappings, J. Funct. Anal. USA, 46, (1982) 126-130. https://doi.org/10.1016/0022-1236(82)90048-9
  29. J.M. Rassias, S. Karthikeyan, G. Ganapathy, M. Suresh, T.R.K. Kumar, Generalized Ulam-Hyers Stability Results of a Quadratic Functional Equation in Felbin’s Type Fuzzy Normed Linear Spaces, Int. J. Anal. Appl. 20 (2022), 15. https://doi.org/10.28924/2291-8639-20-2022-15.
  30. T.M. Rassias, On the Stability of the Linear Mapping in Banach Spaces, Proc. Amer. Math. Soc. 72 (1978), 297–300. 0
  31. Th. M. Rassias: Problem 16; 2, Report of the 27th International Symp. on Functional Equations. Aequationes Math. 39 (1990), 292-293; 309.
  32. K. Ravi, M. Arunkumar, J. M. Rassias, Ulam Stability for the Orthogonally General Euler-Lagrange Type Functional Equation, Int. J. Math. Stat. 3 (2008), 36–46.
  33. T. Salat, On the Statistically Convergent Sequences of Real Numbers, Math. Slovaca. 30 (1980), 139–150. http://dml.cz/dmlcz/136236.
  34. G.L. Sewell, Quantum Mechanics and its Emergent Macrophysics, Princeton University Press, Princeton, 2002.
  35. H. Steinhaus, Sur la Convergence Ordinaire et la Convergence Asymptotique, Colloq. Math. 2 (1951), 73–74.
  36. S.M. Ulam, Problems in Modern Mathematics, John Wiley & Sons, Inc., New York, 1964.
  37. A. Wilansky, Modern Methods in Topological Vector Space, McGraw-Hill, New York, 1978.